Chapter 6 Modeling Cycle
In this chapter we will focus on the cyclical component of a time series and hence focus on data that either has no trend and seasonal components, or data that is filtered to eliminate any trend and seasonality. One of the most commonly used method to model cyclicality is the Autogressive Moving Average (ARMA). This model has two distinct components:
Autoregressive (AR) component: the current period value of a time series variable depends on its past (lagged) observations. We use \(p\) to denote the order of the AR component and is the number of lags of a variable that directly affect the current period value. For example, a firm’s production in the current period maybe impacted by past levels of production. If last year’s production exceeded demand, the stock of unsold goods may be used to meet this period demand first, hence lowering the current period production.
Moving average (MA) component: the current period value of a time series variable depends on current period shock as well as past shocks to this variable. We use \(q\) to denote the order of the MA component and is the number of past period shocks that affect the current period value of the variable of interest. For example, if the Federal Reserve Bank raises the interest in 2016, the effects of that policy shock may impact investment and consumption spending in 2017.
Before we consider these time series model in details it is useful to discuss certain properties of time series that allow us a better understanding of these models.
6.1 Stationarity and Autocorrelation
6.1.1 Covariance Stationary Time Series
Definition 6.1 (Covariance Stationary Time Series)
A time series \(\{y_t\}\) is said to be a covariance stationary process if:
- \(E(y_t)=\mu_y \quad \forall \quad t\)
- \(Var(y_t)=\sigma_y^2 \quad \forall \quad t\)
- \(Cov(y_t,y_{t-s})=\gamma(s) \quad \forall \quad s\neq t\)
One way to think about stationarity is mean-reversion, i.e, the tendency of a time series to return to its long-run unconditional mean following a shock (or a series of shock). Figure @(fig:ch6-figure1) below shows this property graphically.
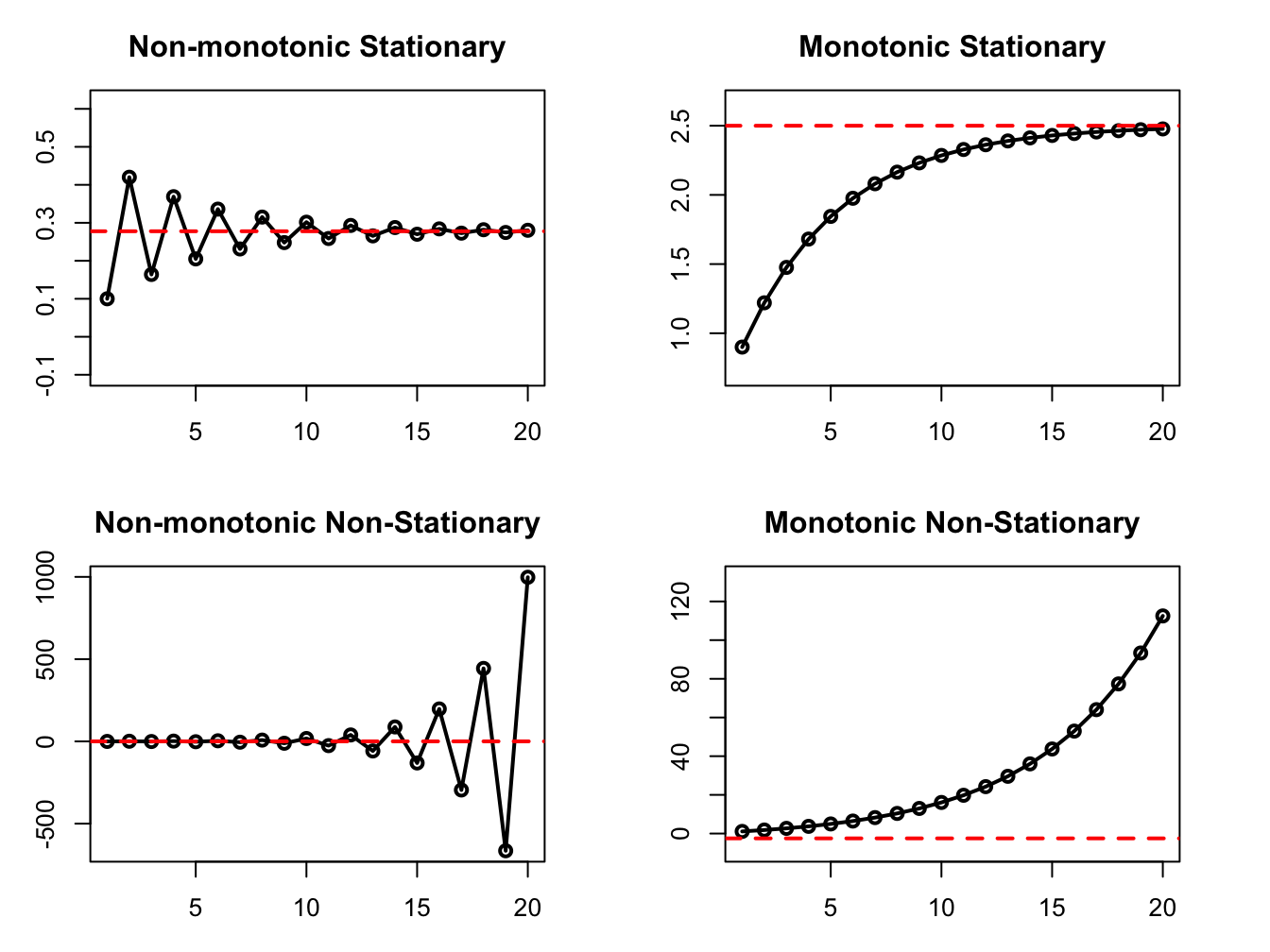
Figure 6.1: Reversion to mean
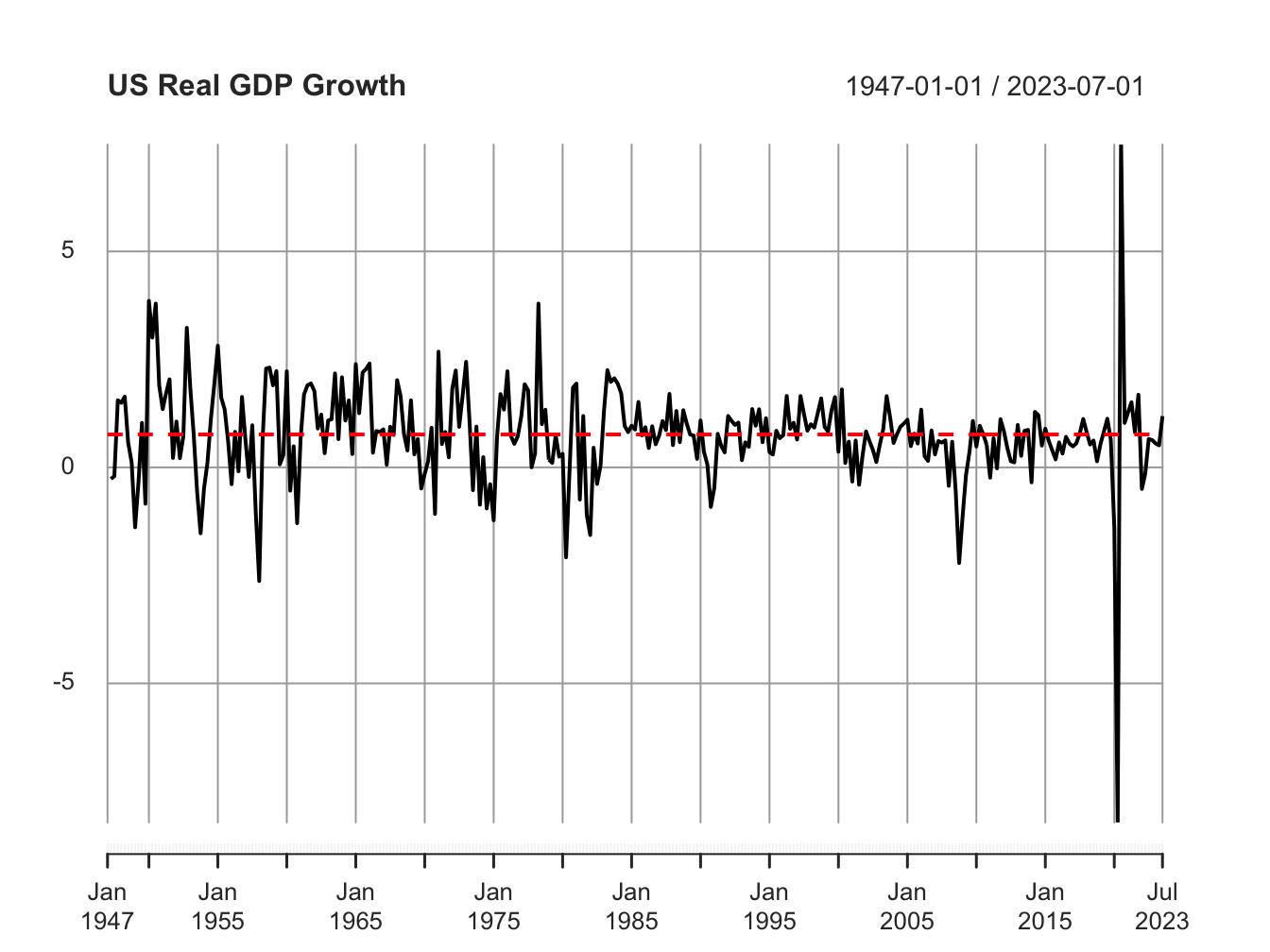
Figure 6.2: Reversion to mean in practice
In practice however, you will not be able to visualize a mean-reverting stationary process this clearly. For example, in Figure 6.2 we plot real GDP growth for the U.S. which is a stationary process with a mean of 0.7%. In this chapter we will only consider stationary time series data. Later on we will learn how to work with non-stationary data.
6.1.2 Correlation vs Autocorrelation
In statistics, correlation is a measure of relationship between two variables. In the time series setting, we can think of the current period value and the past period value of a variable as two separate variables, and compute correlation between them. Such a correlation, between current and lagged observation of a time series is called serial correlation or autocorrelation. In general, for a time series, \(\{y_t\}\), the autocorrelation is given by:
\[\begin{align} Cor(y_t,y_{t-s})=\frac{ Cov(y_t,y_{t-s})}{\sqrt{\sigma^2_{y_t} \times \sigma^2_{y_{t-s}}}} \end{align}\] where \(Cov(y_t,y_{t-s})= E(y_t-\mu_{y_t})(y_{t-s}-\mu_{y_{t-s}})\) and \(\sigma^2_{y_t}=E(y_t-\mu_{y_t})^2\)
For a stationary time series, using the three conditions the Autocorrelation Function (ACF) denoted by \(\rho(s)\) is given by:
\[\begin{align} ACF(s) \ or \ \rho(s)=\frac{\gamma(s)}{\gamma(0)} \end{align}\]
Non-zero values of the ACF indicates presences of serial correlation in the data. Figure 6.3 shows the ACF for a stationary time series with positive serial correlation. If your data is stationary then the ACF should eventually converge to 0. For a non-stationary data, the ACF function will not decay over time.
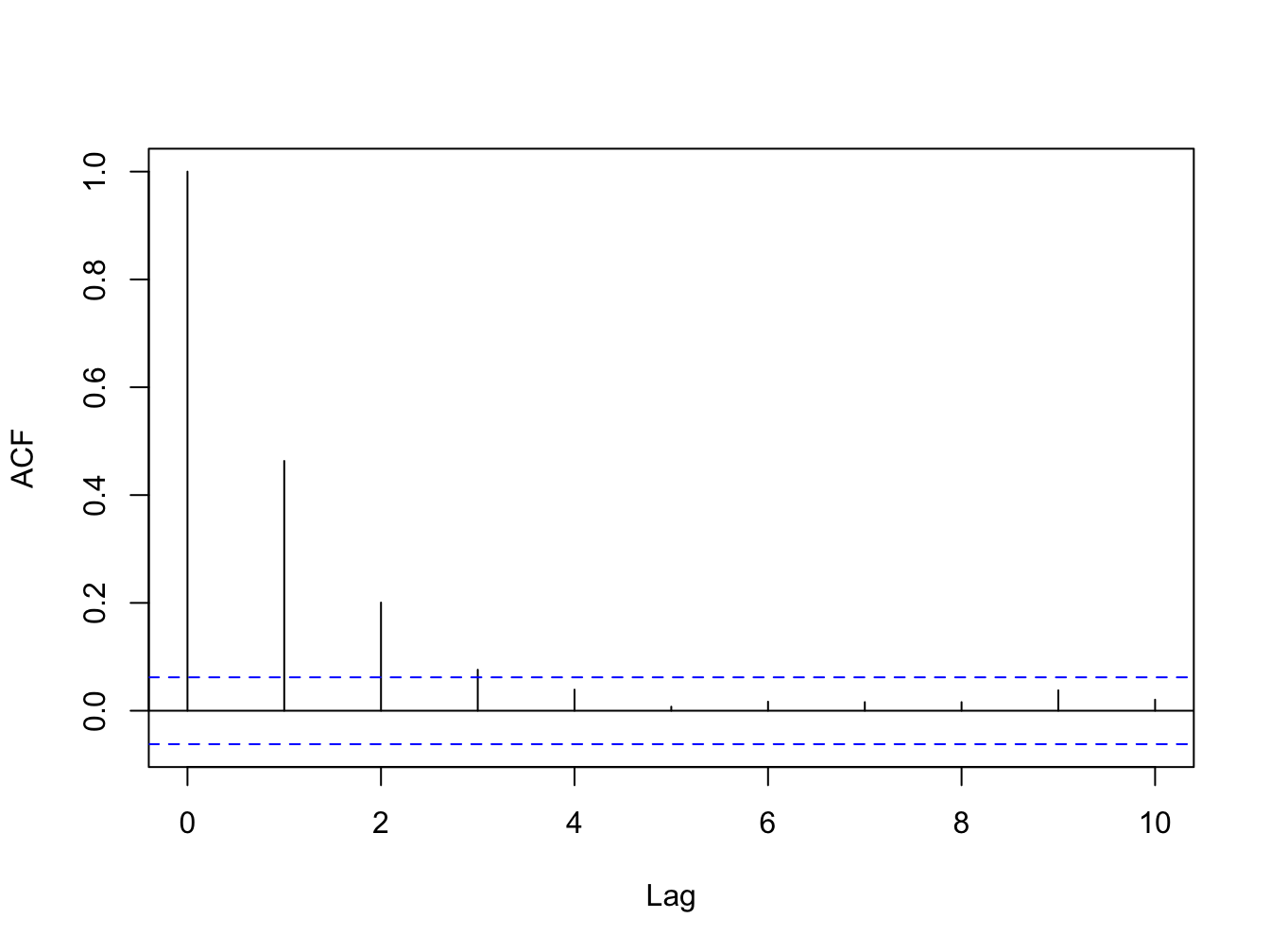
Figure 6.3: ACF for a Stationary Time Series
6.1.3 Partial Autocorrelation
The ACF captures the relationship between the current period value of a time series and all of its past observations. It includes both direct as well as indirect effects of the past observations on the current period value. Often times it is of interest to measure the direct relationship between the current and past observations, partialing out all indirect effects. The partial autocorrelation function (PACF) for a stationary time series \(y_t\) at lag \(s\) is the direct correlation between \(y_t\) and \(y_{t-s}\), after filtering out the linear influence of \(y_{t-1},\ldots,y_{t-s-1}\) on \(y_t\). Figure 6.4 below shows the PACF for a stationary time series where only one lag directly affects the time series in the current period.
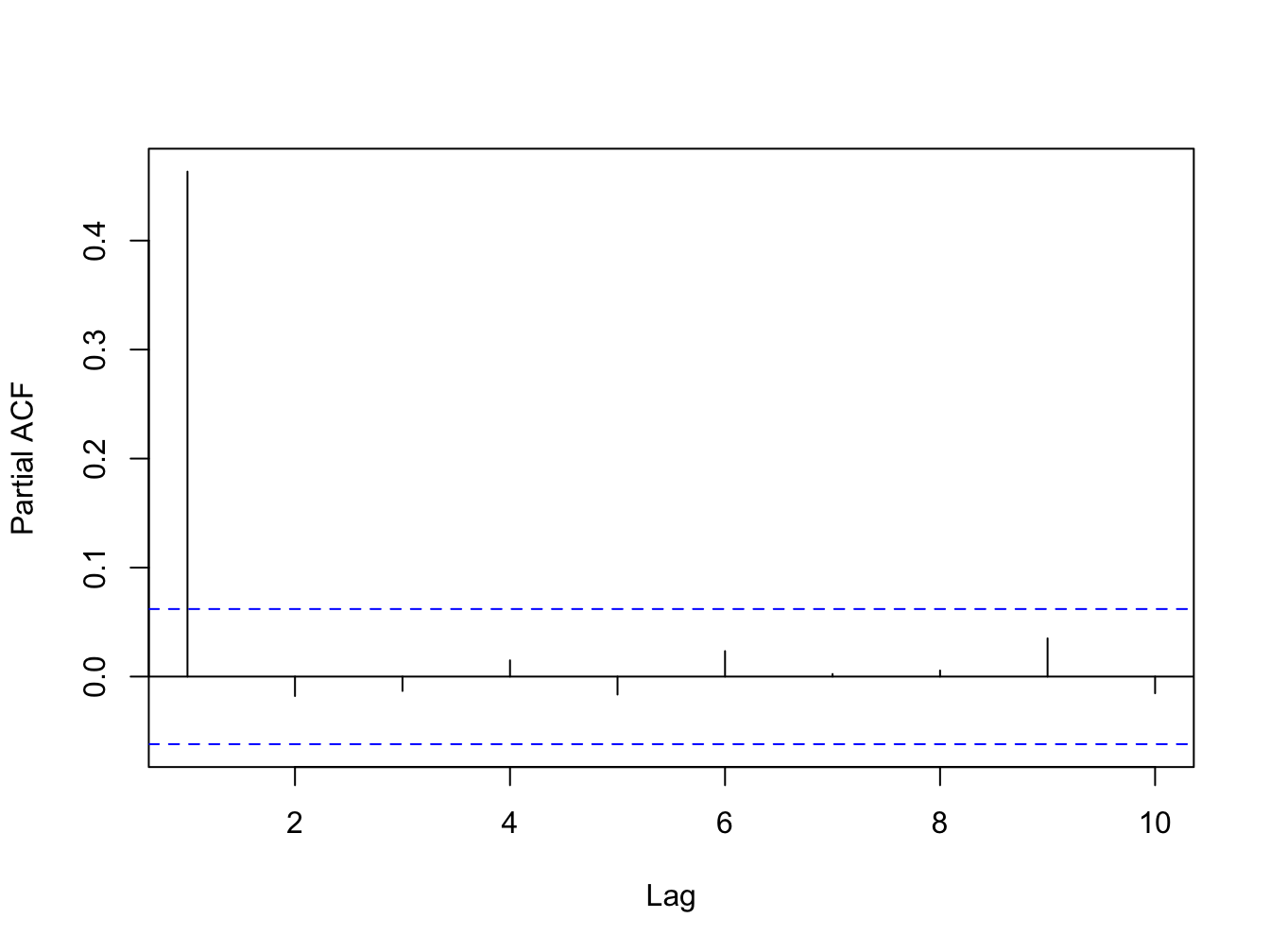
Figure 6.4: PACF for a Stationary Time Series
6.1.4 Lag operator
A lag operator denoted by \(L\) allows us to write ARMA models in a more concise way. Applying lag operator once moves the time index by one period; applying it twice moves the time index back by two period; applying it \(s\) times moves the index back by \(s\) periods. \[ Ly_t=y_{t-1} \] \[ L^2y_t=y_{t-2} \] \[ L^3y_t=y_{t-3} \] \[\vdots\] \[ L^sy_t=y_{t-s} \]
6.2 Autoregressive (AR) Model
A stationarytime series \(\{x_t\}\) can be modeled as an AR process. In general, an AR(p) model is given by:
\[\begin{equation} y_t = \phi_0 +\phi_1 y_{t-1} + \phi_2 y_{t-2} + ...... + \phi_p y_{t-p}+\epsilon_t \end{equation}\]
Here \(\phi_i\) captures the effect of \(y_{t-i}\) on \(y_t\). The order of the AR process is not known apriori. It is common to use either AIC or BIC to determine the optimal lag length for an AR process.
Using the Lag operator, we can rewrite the above AR(p) model as follows: \[ \Phi(L)y_t=\phi_0+\epsilon_t \]
where \(\displaystyle \Phi(L)\) is a polynomial of degree \(p\) in L:
\[ \Phi(L) = 1-\phi_1 L - \phi_2 L^2- \ldots\ldots\ldots\ldots -\phi_p L^p\]
For example, an AR(1) model can be written as: \[y_t=\phi_0+\phi_1 y_{t-1} + \epsilon_t \Rightarrow \Phi(L)y_t=\phi_0+\epsilon_t\] where, \[ \Phi(L) = 1-\phi_1 L \]
Characteristic equation: A characteristic equation is given by:
\[\Phi(L)=0\]
The roots of this equation play an important role in determining the dynamic behavior of a time series.
6.2.1 Unit root and Stationarity
For a time series to be stationary there should be no unit root in its characteristic equation. In other words, all roots of the characteristic equation must fall outside the unit circle. Consider the following AR(1) model: \[\Phi(L)y_t = \phi_0 + \epsilon_t\]
The characteristic equation is given by: \[\Phi(L)=1-\phi_1L=0 \]
The root that satisfies the above equation is: \[ L^*=\frac{1}{\phi_1}\]
For no unit root to be present, \(L^*>|1|\) which implies that \(|\phi_1|<1\).
Typically, for any AR process to be stationary, some restrictions will be imposed on the values of \(\phi_i's\), the coefficients of the lagged variables in the model.
6.2.2 Properties of an AR(1) model
A stationary AR(1) model is given by: \[ y_t=\phi_0 +\phi_1 y_{t-1}+ \epsilon_t \quad ; \ \epsilon_t\sim WN(0, \sigma_\epsilon^2) \ and \ |\phi_1|<1\]
\(\displaystyle \phi_1\) measures the persistence in data. A larger value indicates shocks to \(y_t\) dissipate slowly over time.
Stationarity of \(y_t\) implies certain restrictions on the AR(1) model.
- Constant long run mean: is the unconditional expectation of \(y_t\): \[ E(y_t) = \mu_y= \frac{\phi_0}{1-\phi_1} \]
- Constant long run variance: is the unconditional variance of \(y_t\): \[ Var(y_t)=\sigma^2_y= \frac{\sigma^2_\epsilon}{1-\phi_1^2}\]
- ACF function: \[ \rho(s) = \phi_1^s\]
- PACF function: \[\begin{equation*} PACF(s) = \begin{cases} \phi_1 & \text{if s=1}\\ 0 & \text{if s>1} \end{cases} \end{equation*}\]
6.3 Estimating an AR model
When estimating the AR model we have two alternatives:
OLS: biased (but consistent) estimates. Also, later on when we add MA components we cannot use OLS.
Maximum Likelihood Estimation (MLE): can be used to estimate AR as well as MA components
6.3.1 Maximum Likelihood Estimation (MLE)
- MLE approach is based on the following idea:
what set of values of our parameters maximize the likelihood of observing our data if the model we have was used to generate this data.
Likelihood function: is a function that gives us the probability of observing our data given a model with some parameters.
6.3.1.1 Likelihood vs Probability
Consider a simple example of tossing a coin. Let \(X\) denotes the random variable that is the outcome of this experiment being either heads or tails. Let \(\theta\) denote the probability of heads which implies \(1-\theta\) is the probability of obtaining tails. Here, \(\theta\) is our parameter of interest. Suppose we toss the coin 10 times and obtain the following data on \(X\): \[X=\{H,H,H,H,H,H,T,T,T,T\}\]
Then, the probability of obtaining this sequence of X is given by: \[Prob (X|\theta)=\theta^6 (1-\theta)^4\]
This is the probability distribution function the variable \(X\). As we change \(X\), we get a different probability for a given value of \(\theta\).
Now let us ask a different question. Once we have observed the sequence of heads and tails, lets call it our data which is fixed. Then, what is probability of observing this data, if our probability distribution function is given by the equation above? That gives us the likelihood function:
\[ L(\theta)=Prob(X|\theta)=\theta^6(1-\theta)^4\]
Note that with fixed \(X\), as we change \(\theta\) the likelihood of observing this data will change.
This is an important point that distinguishes likelihood function from the probability distribution function. Although both have the same equation, the probability function is a function of the data with the value of the parameter fixed, while the likelihood function is a function of the parameter with the data fixed.
6.3.1.2 Maximum Likelhood Estimation
Now we are in a position to formally define the likelihood function.
Definition 6.2 Let \(X\) denotes a random variable with a given probability distribution function denoted by \(f(x_i|\theta)\). Let \(D=\{x_1, x_2,\dots,x_n\}\) denote a sample realization of \(X\). Then, the likelhood function, denoted by \(L(\theta)\) is given by: \[L(\theta)=f(x_1,x_2,\dots,x_n|\theta)\]
If we further assume that each realization of \(X\) is independent of the others, we get: \[L(\theta)=f(x_1,x_2,\dots,x_n|\theta)=f(x_1|\theta)\times f(x_2|\theta) \times \dots \times f(x_n|\theta)\]
A mathematical simplification is to work with natural logs of the likelihood function, which assuming independently distributed random sample, gives us:
\[ lnL(\theta)=ln(f(x_1|\theta)\times f(x_2|\theta) \times \dots \times f(x_n|\theta))=\sum_{i=1}^{N}ln(f(x_i|\theta))\]
Definition 6.3 The maximum likelihood estimator, denoted by \(\hat{\theta}_{MLE}\), maximizes the log likelihood function: \[ \hat{\theta}_{MLE} \equiv arg \max_{\theta} lnL(\theta) \]
Example 6.1 Compute maximum likelihood estimator of \(\mu\) of an indpendently distributed random variable that is normally distributed with a mean of \(\mu\) and a variance of \(1\):
\[ f(y_t|\mu)=\frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2} (y_t-\mu)^2}\]
Solution: The log likelihood function is given by:
\[lnL= -Tln2\pi-\frac{1}{2}\sum_{t=1}^T(y_t-\mu)^2 \]
From the first order condition, we get \[ \frac{\partial LnL}{\partial \mu}=\sum_{t=1}^T(y_t-\mu)=0\Rightarrow \hat{\mu}_{MLE}=\frac{\sum_{t=1}^T y_t}{T}\]
6.3.2 MLE of an AR(p) model
One complication we face in estimating an AR(p) model is that by definition the realizations of the variable are not independent of each other. As a result we cannot simplify the likelihood function by multiplying individual probability density functions to obtain the joint probability density function, i.e., \[ f(y_1,y_2,\dots,y_T|\theta) \neq f(y_1|\theta)\times f(y_2|\theta)\times \dots \times f(y_T|\theta)\]
Furthermore, as the order of AR increases, the joint density function we need to estimate becomes even more complicated. In this class we will focus on the method that divides the joint density into the product of conditional densities and density of a set of initial values. The idea comes from the conditional probability formula for two related events \(A\) and \(B\):
\[ P(A|B) =\frac{P(\text{A and B})}{P(B)} \Rightarrow P(\text{A and B}) = P(A|B)\times P(B) \]
In the time series context, I will explain this for a stationary AR(1) model. We know that in this model only last period observation directly affects the current period value. Hence, consider the first two observations of a stationary time series: \(y_1\) and \(y_2\). Then the joint density of these adjacent observations is given by,
\[ f(y_1,y_2;\theta)= f(y_2|y_1; \theta)\times f(y_1;\theta)\]
Similarly, for the first three observations we get:
\[ f(y_1,y_2,y_3;\theta)= f(y_3|y_2; \theta)\times f(y_2|y_1; \theta) \times f(y_1; \theta)\]
Hence, for \(T\) observations we get:
\[ f(y_1,y_2,y_3, ...,y_T; \theta)= f(y_T|y_{T-1};\theta)\times f(y_{T-1}|y_{T-2}; \theta)\times.... \times f(y_1; \theta)\]
The log-likelihood function is given by:
\[ ln \ L(\theta) = ln \ f(y_1;\theta) + \sum_{t=2}^{T} ln \ f(y_t|y_{t-1}; \theta) \]
We can then maximize the above likelihood function to obtain an MLE estimator for the AR(1) model.
6.3.3 Selection of optimal order of the AR model
Note that apriori we do not know the order of the AR model for any given time series. We can determine the optimal lag order by using either AIC or BIC. The process is as follows:
Set \(p=p_{max}\) where \(p_{max}\) is an integer. A rule of thumb is to set \[p_{max}=integer\left[12\times \left(\frac{T}{100}\right)^{0.25}\right]\]
Estimate all AR models from \(p=1\) to \(p=p_{max}\).
Select the final model as the one with lowest AIC or lowest BIC.
6.3.4 Forecasting using AR(p) model
Having estimated our AR(p) model with the optimal lag length, we can use the conditional mean to compute the forecast and conditional variance to compute the forecast errors. Consider an AR(1) model:
\[y_t=\phi_0+\phi_1 y_{t-1} +\epsilon_t\]
Then, the 1-period ahead forecast is given by: \[f_{t,1}=E(y_{t+1}|\Omega_t)=\phi_0+\phi_1 y_t\] Similarly, the 2-period ahead forecast is given by: \[f_{t,2}=E(y_{t+2}|\Omega_t)=\phi_0+\phi_1 E(y_{t+1}|\Omega_t) =\phi_0+\phi_1f_{t,1}\]
In general, we can get the following recursive forecast equation for h-period’s ahead: \[f_{t,h}=\phi_0+\phi_1 f_{t,h-1}\]
Correspondingly, the h-period ahead forecast error is given by: \[e_{t,h}=y_{t+h}- f_{t,h}=\epsilon_{t+h}+\phi_1 e_{t,h-1}\]
Theorem 6.1 The h-period ahead forecast converges to the unconditional mean of \(y_t\), i.e., \[\lim_{h\to\infty} f_{t,h}=\mu_y=\frac{\phi_0}{1-\phi_1}\]
Theorem 6.2 The variance of the h-period ahead forecast error converges to the unconditional variance of \(y_t\), i.e., \[\lim_{h\to\infty} Var(e_{t,h})=\sigma^2_y=\frac{\sigma^2_\epsilon}{1-\phi_1^2}\]
6.4 Moving Average (MA) Model
Another commonly used method for capturing the cyclical component of the time series is the moving average (MA) model where the current value of a time series linearly depends on current and past shocks. Formally, a stationary time series \(\{y_t\}\) can be modeled as an MA(q) process: \[\begin{equation} y_t = \theta_0 + \epsilon_t + \theta_1 \epsilon_{t-1} + \theta_2 \epsilon_{t-2} + ...... + \theta_q \epsilon_{t-q} \end{equation}\]
Using lag operator, we can write this in more compact form as:
\[y_t = \theta_0 +\Theta(L) \epsilon_t\]
where \(\Theta(L)=1+\theta_1 L+ \theta_2 L^2+...+\theta_q L^q\) is lag polynomial of order \(q\).
Note that because each one of the current and past shocks are white noise processes, an MA(q) model is always stationary.
6.4.1 Invertibility of an MA process
Consider the following MA(1) process with\(\theta_0=0\) for simplicity: \[y_t=\epsilon_t +\theta_1 \epsilon_{t-1}\]
Using the lag operator we can rewrite this equation as follows:
\[y_t= (1+\theta_1L)\epsilon_t \Rightarrow y_t(1+\theta_1 L) ^{-1}=\epsilon_t\]
Note that if \(|\theta_1|<1\), then we can use the Taylor series expansion centered at 0 and get:
\[(1+\theta_1 L)^{-1}=1-\theta_1 L+(\theta_1L)^2-(\theta_1L)^3+ (\theta_1L)^4-...... \]
Hence, an MA(1) can be rewritten as follows:
\[y_t (1-\theta_1 L+(\theta_1L)^2-(\theta_1L)^3+ (\theta_1L)^4-......)=\epsilon_t\] \[\Rightarrow y_t -\theta_1 y_{t-1} +\theta_1^2y_{t-2}-\theta_1^3 y_{t-3}....=\epsilon_t\]
Rearranging terms, we get the \(AR(\infty)\) representation for an invertible MA(1) model: \[y_t=-\sum_{i=1}^{\infty}(-\theta_1)^i \ y_{t-i}+\epsilon_t\]
Definition 6.4 An MA process is invertible if it can be represented as a stationary \(AR(\infty)\).
6.4.2 Properties of an invertible MA(1)
An invertible MA(1) model is given by:
\[ y_t = \theta_0 + \epsilon_t + \theta_1 \epsilon_{t-1} \quad ; \ \epsilon_t\sim WN(0, \sigma_\epsilon^2) \ and \ |\theta_1|<1\]
Constant unconditional mean of \(y_t\): \[E(y_t)=\mu_y =\theta_0 \]
Constant unconditional variance of \(y_t\):
\[Var(y_t)=\sigma^2_y=\sigma^2_\epsilon(1+\theta_1^2)\]
ACF function: \[\begin{equation*} ACF(s) = \begin{cases} \frac{\theta_1}{1+\theta_1^2} & \text{if s=1}\\ 0 & \text{if s>1} \end{cases} \end{equation*}\]
PACF function: using the invertibility it is evident that PACF of an MA(1) decays with \(s\).
6.4.3 Forecast based on MA(q)
Like before, the h-period ahead forecast is the conditional expected value of the time series. Consider an MA(1) model:
\[y_t=\theta_0 +\epsilon_t + \theta_1 \epsilon_{t-1}\]
Then, the 1-period ahead forecast is given by:
\[f_{t,1}=E(y_{t+1}|\Omega_t)=\theta_0+ \theta_1 \epsilon_{t-1}\]
The h-period ahead forecast for \(h>1\) is given by: \[f_{t,h}=E(y_{t+h}|\Omega_t)=\theta_0\]
In general, for an MA(q) model, the forecast for \(h>q\) is the long run mean \(\theta_0\). This is why we say that an MA(q) process has a memory of q periods.
6.5 ARMA(p, q)
An ARMA model simply combines both AR and MA components to model the dynamics of a time series. Formally,
\[\begin{equation} y_t = \phi_0 +\phi_1 y_{t-1} + \phi_2 y_{t-2} + ...... + \phi_p y_{t-p}+\epsilon_t + \theta_1 \epsilon_{t-1} + \theta_2 \epsilon_{t-2} + ...... + \theta_q \epsilon_{t-q} \end{equation}\]
Note that:
Estimation is done by maximum likelihood method.
Optimal order for AR and MA components is selected using AIC and/or BIC.
The forecast of \(y_t\) from an ARMA(p,q) model will be dominated by the AR component for \(h>q\). To see this consider the following ARMA(1,1) model:
\[y_t = \phi_0 +\phi_1 y_{t-1}+ \epsilon_t + \theta_1 \epsilon_{t-1}\]
Then, the 1-period ahead forecast is: \[f_{t,1} = E(y_{t+1}|\Omega_t) = \phi_0 + \phi_1 y_t + \theta_1 \epsilon_{t-1}\]
Here both MA and AR component affect the forecast. But now consider the 2-period ahead forecast:
\[f_{t,2} = E(y_{t+2}|\Omega_t) = \phi_0 + \phi_1 f_{t,1}\]
Hence, no role is played by the MA component in determining the 2-period ahead forecast. For any \(h>1\) only the AR component affects the forecast from this model.
6.6 Integrated ARMA or ARIMA(p,d,q)
Thus far we have assumed that our data is stationary. However, often we may find that this assumption is not supported in practice. In such a case we need to tranform our data appropriately before estimating an ARMA model. The procedure can be summarized as follows:
Determine whether there is a unit root in data or not. Presence of unit root indicates non-stationarity. We will use Augmented Dickey-Fuller (ADF) test for this purpose.
If data is non-stationary, then we need to appropriately transform our data to make it stationary.
Once we have obtained a stationary transformation of our original data, we can proceed and estimate the ARMA model as before.
6.7 Trend Stationary vs Difference Stationary Time Series
There are two types of time series we often encounter in real world:
- Trend-stationary: a time-series variable is non-stationary becuase it has a deterministic trend. Once we detrend our data then it will become stationary. In this case the appropriate transformation is to estimate a trend model and then use the residual as the detrended stationary data. For example, suppose our data has a linear trend given by:
\[y_t = \beta_0 +\beta_1 t +\epsilon_t\]
Then the OLS residual from this model, \(e_t=y_t-\hat{y_t}\) is the detrended \(y_t\) which will be stationary. Hence, we will estimate an ARMA(p,q) model using this detrended variable.
- Difference-stationary: a time-series variable is non-stationary because it contains a stochastic trend. Here, the transformation requires us to difference the orignial data until we obtain a stationary time series. Let \(d\) denote the minimum number of differences needed to obtain a stationary time series:
\[\Delta_d \ y_t=(1-L)^d \ y_t\]
In this case, we say that \(y_t\) is intergrated of order \(d\) or more formally, \(y_t\) is an \(I(d)\) process. Hence, for \(d=1\) we obtain an \(I(1)\) process implying that:
\[\Delta_1 \ y_t=(1-L)^1 \ y_t=y_t-y_{t-1} \quad \text{is stationary}\]
In otherwords, the first difference of an I(1) process is stationary. Similarly for \(d=2\), we obtain an \(I(2)\) process where second difference will be stationary and so forth.
6.8 Testing for a unit root
Consider the following AR(1) model with no trend and intercept:
\[y_t=\phi_1 y_{t-1} +\epsilon_t \ quad ; \epsilon_t\sim WN(0,\sigma^2_\epsilon)\]
We know that if \(\phi_1=1\) we have a unit root in this data. Lets subtract \(y_{t-1}\) from both sides and rewrite this model as:
\[y_t-y_{t-1}= (\phi_1-1)y_{t-1}+\epsilon_t \]
Define \(\rho=phi_1-1\). Then, we get: \[\Delta y_t= \rho \ y_{t-1}+\epsilon_t \]
We can now estimate the above model and carry out the following test known as the Dickey-Fuller (DF) test:
\[H_0: \rho=0 \] \[H_A: \rho<0\]
If the null hypothesis is not rejected, then we do not have sample evidence against the statement that \(\rho=0 \Rightarrow \phi_1=1\). Hence, we conclude that there is no evidence against the statement that there is unit root in the data. In contrast, if we reject the null hypothesis, then we can conclude that there is no unit root and hence the data is stationary.
The t- statistic is for the above test is denoted by \(\tau_1\) and is given by: \[\tau_1 =\frac{\hat{\rho}}{se(\hat{\rho})}\]
Under the null hypothesis this test statistic follows the DF-distribution and the critical values are provided in most statistical softwares. Given that this is a left-tail test, the decision rule is that if the test statistic is less than the critical value then we reject the null hypothesis.
There are two issues we face when implementing this test in practice:
First, the above procedure assumes that there is no intercept and trend in the data. In real world, we cannot make that assumption and must extend the test procedure to accomodate a non-zero intercept and trend. Hence, we have the following two additional versions of the DF test:
- Constant and no trend model: Here our AR(1) model is
\[\Delta y_t= \phi_0 + \rho \ y_{t-1}+\epsilon_t \]
Now we can do two possible tests. The first test is that of the unit root:
\[H_0: \rho=0 \] \[H_A: \rho<0\]
The t statistic for this test is denoted by \(\tau_2\) and is given by: \[\tau_2 =\frac{\hat{\rho}}{se(\hat{\rho})}\]
If the test statisitic is less than the critical value, we reject the null.
The second test we can do is: \[H_0: \rho=\phi_0=0 \] \[H_A: Not \ H_0\] The test statistic for this test is denoted by \(\phi_1\). If the test statistic exceeds the critical value then we reject the null.
- Constant and linear trend model: Here our AR(1) model is
\[\Delta y_t= \phi_0 + \beta \ t+ \rho \ y_{t-1}+\epsilon_t \]
Now we can do three possible tests. The first test is that of the unit root; \[H_0: \rho=0 \] \[H_A: \rho<0\] The t statistic for this test is denoted by \(\tau_3\) and is given by:
\[\tau_3 =\frac{\hat{\rho}}{se(\hat{\rho})}\]
If the test statisitic is less than the critical value, we reject the null.
The second test is: \[H_0: \rho=\phi_0=\beta=0 \] \[H_A: Not \ H_0\] The test statistic for this test is denoted by \(\phi_2\). If the test statistic exceeds the critical value then we reject the null.
Finally the third test is: \[H_0: \rho=\beta=0 \] \[H_A: Not \ H_0\] The test statistic for this test is denoted by \(\phi_3\). If the test statistic exceeds the critical value then we reject the null.
Second, we only have allowed for AR(1). We need to extend the above testing procedure for higher order AR models. The Augmented DF (ADF) test allows for higher order lags in testing for a unit root. For example, the model with an intercept, trend, and \(p\) lags is given by: \[\Delta y_t= \phi_0 + \beta \ t+ \rho \ y_{t-1}+\sum_{i=2}^p\delta_i y_{t-i}+\epsilon_t \quad where \ \rho=\sum_{i=1}^p \phi_i-1\]
6.8.1 Testing for unit root in USD/CAD exchange rate
In this application we will test for unit root in US-Canada exchange rate. For this purpose we work with monthly data from Jan 1971 through Oct 2018. Below I show the results for 3 models using the urca package in R.
##
## ###############################################
## # Augmented Dickey-Fuller Test Unit Root Test #
## ###############################################
##
## Test regression none
##
##
## Call:
## lm(formula = z.diff ~ z.lag.1 - 1 + z.diff.lag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.069820 -0.009107 0.000237 0.010474 0.125124
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## z.lag.1 0.0001568 0.0005601 0.28 0.78
## z.diff.lag 0.2574519 0.0385402 6.68 5.24e-11 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.01746 on 632 degrees of freedom
## Multiple R-squared: 0.06634, Adjusted R-squared: 0.06338
## F-statistic: 22.45 on 2 and 632 DF, p-value: 3.8e-10
##
##
## Value of test-statistic is: 0.28
##
## Critical values for test statistics:
## 1pct 5pct 10pct
## tau1 -2.58 -1.95 -1.62##
## ###############################################
## # Augmented Dickey-Fuller Test Unit Root Test #
## ###############################################
##
## Test regression drift
##
##
## Call:
## lm(formula = z.diff ~ z.lag.1 + 1 + z.diff.lag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.067869 -0.009589 -0.000771 0.009999 0.123380
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.011288 0.005352 2.109 0.0353 *
## z.lag.1 -0.008878 0.004320 -2.055 0.0403 *
## z.diff.lag 0.261053 0.038473 6.785 2.67e-11 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.01742 on 631 degrees of freedom
## Multiple R-squared: 0.07208, Adjusted R-squared: 0.06914
## F-statistic: 24.51 on 2 and 631 DF, p-value: 5.61e-11
##
##
## Value of test-statistic is: -2.0552 2.2637
##
## Critical values for test statistics:
## 1pct 5pct 10pct
## tau2 -3.43 -2.86 -2.57
## phi1 6.43 4.59 3.78##
## ###############################################
## # Augmented Dickey-Fuller Test Unit Root Test #
## ###############################################
##
## Test regression trend
##
##
## Call:
## lm(formula = z.diff ~ z.lag.1 + 1 + tt + z.diff.lag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.067861 -0.009434 -0.000801 0.009864 0.123206
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.136e-02 5.364e-03 2.117 0.0346 *
## z.lag.1 -9.173e-03 4.505e-03 -2.036 0.0422 *
## tt 9.159e-07 3.941e-06 0.232 0.8163
## z.diff.lag 2.613e-01 3.852e-02 6.784 2.7e-11 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.01743 on 630 degrees of freedom
## Multiple R-squared: 0.07216, Adjusted R-squared: 0.06775
## F-statistic: 16.33 on 3 and 630 DF, p-value: 3.114e-10
##
##
## Value of test-statistic is: -2.0362 1.5249 2.1357
##
## Critical values for test statistics:
## 1pct 5pct 10pct
## tau3 -3.96 -3.41 -3.12
## phi2 6.09 4.68 4.03
## phi3 8.27 6.25 5.34For the first model with no constant and trend, the test statistic \(\tau_1= 0.2469\) and the 5% critical value is -1.95. For the second model with a constant, the test statistics is \(\tau_2= -1.9315\) and the 5% critical value is -2.86. Finally, for the third model with a trend, the test statistic \(\tau_3= -1.8839\) and the 5% critical value is -3.41. In each, because the test statistic is greater than the critical value, we do not reject the null hypothesis and conclude there is unit root.
6.9 Box-Jenkins Method for estimating ARIMA(p,d,q)
Box-Jenkins is a three-step procedure for finding the best fitting ARIMA(p,d,q) for a non-statinary time series.
Model identification: here we determine the order of integration \(d\), and the optimal number of AR and MA components, \(p\) and \(q\) respectively.
To determine \(d\), we conduct ADF test on successive differences of the original time series. The order of integration is the number times we difference our data to obtain stationarity.
This is followed by estimating ARMA model for different combinations of \(p\) and \(q\). The optimal structure is chosen using either AIC or BIC.
Parameter estimation: we estimate the identified model from the previous step using ML estimation.
Model Evaluation: mostly showing that the residuals from the optimal model is a white noise process. We can do this by using the Breusch-Godfrey LM test of serial correlation for the residuals. If residuals from the final model are white noise then there should be no serial correlation.